Introduction to Complex Math
It turns out the complex form of the equations makes things a lot simpler and more elegant. As such,
everyone uses complex numbers, from physicists, to engineers, and mathematicians. So get used to it,
it is actually a very beautiful thing.
On this page we'll start by introducing complex numbers and some simple properties, useful in the
study of the Fourier Transform.
A complex number z can be written in standard form as:
The complex number z has a real part given by x and an imaginary part
given by y. The real part of z is written as:
The imaginary part of z is written as:
In equations [1,2,3], i is given as:
Example. Z = 4 + i5 ==> Then Re[Z]=4, Im[Z]=5.
Addition and subtraction are straightforward. The addition of two complex numbers (z1 and z2) are the sums
of their real and imaginary parts:
Subtraction can be performed in a similar manner to equation [5]. Multiplication of complex numbers follows
algebra-style rules:
Division will be discussed after the polar representation for complex numbers.
The magnitude of a complex number z is given by:
Equation [9] can be derived by expanding the left side in a Taylor series (with variable theta). Then
expand the right side using the Taylor series expansions for cosine and sine and the results are identical.
The polar form of a complex number is written with a magnitude and angle:
Using equation [9], the polar form can be converted back into it's real and imaginary parts:
The angle theta of the complex number can be determined from the real and imaginary part:
The angle theta is zero when the real part of a complex number is positive and the imaginary part is zero.
The angle theta is 90 degrees when the imaginary part is positive and the real part is zero.
Hence, we can convert between the rectangular form (real and imaginary part) and the polar form (magnitude and angle).
As an example, consider the complex number z=3+i4. This number can be plotted along the x- and y- axis,
as shown in Figure 1. Note that x represents the real part of z, and y represents the imaginary part of z.
Figure 1. Illustration of a Complex Number in the Complex Plane.
In Figure 1, |z|=5 (from equation [8]), and theta=53.13 degrees (from equation [12]).
The polar form makes division very simple.
Example Suppose z1=1+i3, and z2 = -1 - i1. What is (z1 * z2) and z1/z2?
Solution The numbers z1 and z2 are converted to polar form:
|z2|=1.41, theta2 = 225.0 degrees.
Then:
Fourier Transforms are performed using complex numbers. Since Fourier Transforms are used to analyze
real-world signals, why is it useful to have complex (or imaginary) numbers involved at all?  [1]
[1] [2]
[2] [3]
[3] [4]
[4] Addition and Multiplication
 [5]
[5]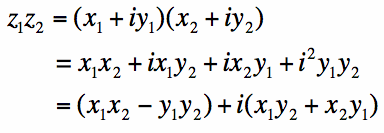 [6]
[6]Complex Conjugate and Magnitude
The complex conjugate of a complex number can be found by replacing the i in equation [1]
with -i. The complex conjugate operator is written as a *, as shown in equation [7]: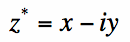 [7]
[7] [8]
[8]Polar Form
The above notation for complex numbers, using real and imaginary parts, is often called standard or rectangular
form. Another common way to express complex numbers is polar form. Before, this is presented,
please recall Euler's identity (which is one of the greatest equations of all time and should be memorized): [9]
[9] [10]
[10] [11]
[11] [12]
[12]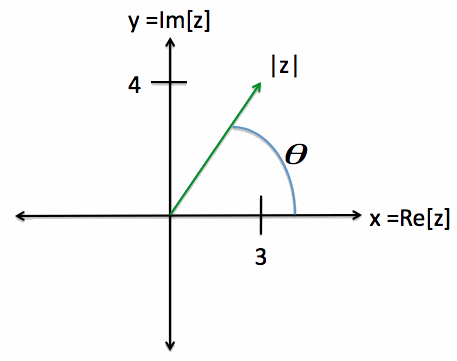
Division
Division can be performed easily using the polar form for complex numbers (multiplication is easier too).
For complex numbers z1 and z2: [13]
[13]
Next: The Impulse
Back: Fourier Transform Mathematical Topics
The Fourier Transform (Home)