Introduction to the Fourier Transform Fourier Series Fourier Transform - Properties Fourier Transform Pairs Fourier Transform Applications Mathematical Background External Links The Fourier Transform is a tool that breaks a waveform (a function or signal) into an alternate representation, characterized by the sine and cosine functions of varying frequencies. The Fourier Transform shows that any waveform can be re-written as the sum of sinusoidals. If you know nothing about Fourier Transforms, start with the Introduction link on the left. If you want to brush up, check the Fourier Transform Properties link. And if you're just looking for a table of Fourier Transforms with derivations, check out the Fourier Transform Pairs link.

This website is intended to be a source of knowledge for learning about and understanding the Fourier Transform. The goal is to present a comprehensive tutorial on the Fourier transform and related topics. In the spirit of Einstein: "Everything should be made as simple as possible, but not simpler." This website will strive to make The Fourier Transform understandable, without unnecessary complexity.

Check out our partner site, antenna-theory.com, the best page on antennas in the world! Fun Fact: Did you know that the radiation pattern of an antenna is often simply the Fourier Transform of the antenna's current distribution? 1. Introduction to the Fourier Transform Virtually everything in the world can be described via a waveform - a function of time, space or some other variable. For instance, sound waves, electromagnetic fields, the elevation of a hill versus location, a plot of VSWR versus frequency, the price of your favorite stock versus time, etc. The Fourier Transform gives us a unique and powerful way of viewing these waveforms. The purpose of this entire website is to explain the following fundamental fact: One of the Fundamental Secrets of the Universe All waveforms, no matter what you scribble or observe in the universe, are actually just the sum of simple sinusoids of different frequencies. The above fact, is exceedingly cool, as we will see. The Fourier Transform decomposes a waveform - basically any real world waveform, into sinusoids. That is, the Fourier Transform gives us another way to represent a waveform. (Need a refresher on sinusoids? 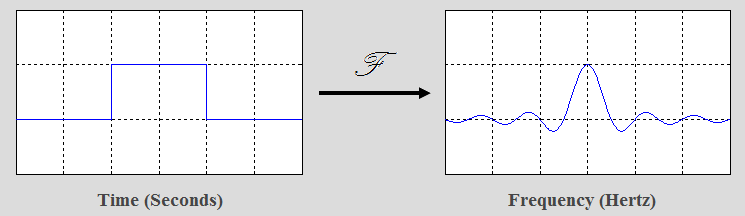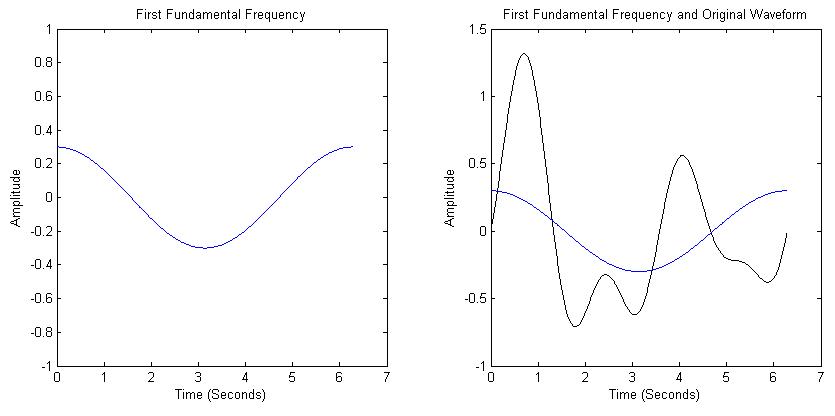See Sinusoid Properties) As an example, lets break down the waveform in Figure 1 into its 'building blocks' (or constituent frequencies). This decomposition can be done with a Fourier transform (or Fourier series for periodic waveforms), as we will see. The first component is a sinusoidal wave with period T=6.28 (2*pi) and amplitude 0.3, as shown in Figure 1.

Figure 1. First fundamental frequency (left) and original waveform (right) compared.

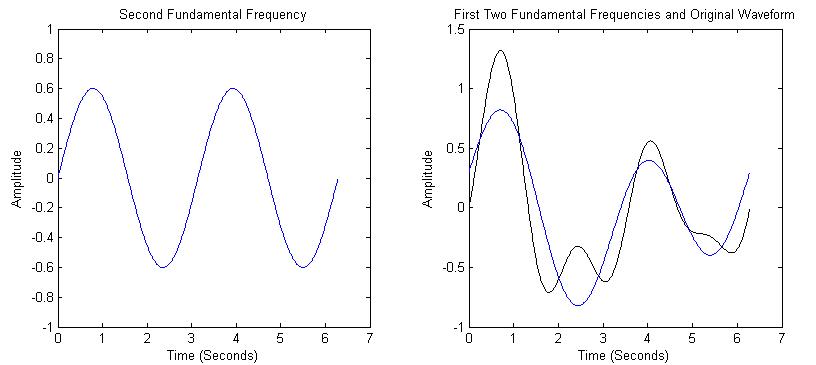
The second frequency will have a period half as long as the first (twice the frequency). The second component is shown on the left in Figure 2, along with the sum of the first two frequencies compared to the original waveform.

Figure 2. Second fundamental frequency (left) and original waveform compared with the first two frequency components.

We see that the sum of the first two frequencies is starting to look like the original waveform. The third frequency component is 3 times the frequency as the first. The sum of the first 3 components are shown in Figure 3.

Figure 3. Third fundamental frequency (left) and original waveform compared with the first three frequency components.

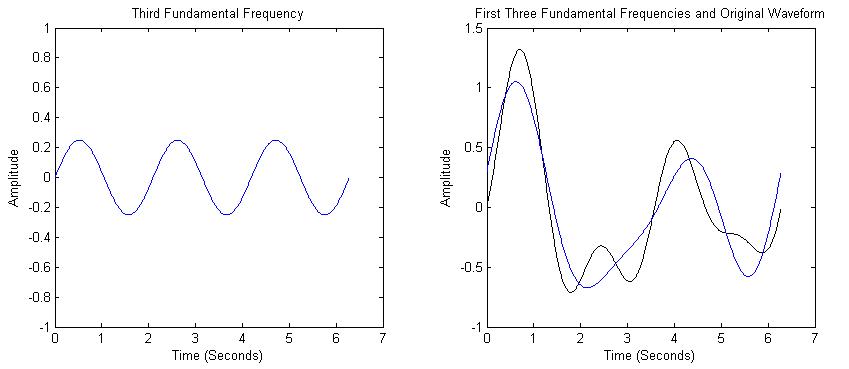
Finally, adding in the fourth frequency component, we get the original waveform, shown in Figure 4.

Figure 4. Fourth fundamental frequency (left) and original waveform compared with the first four frequency components (overlapped).

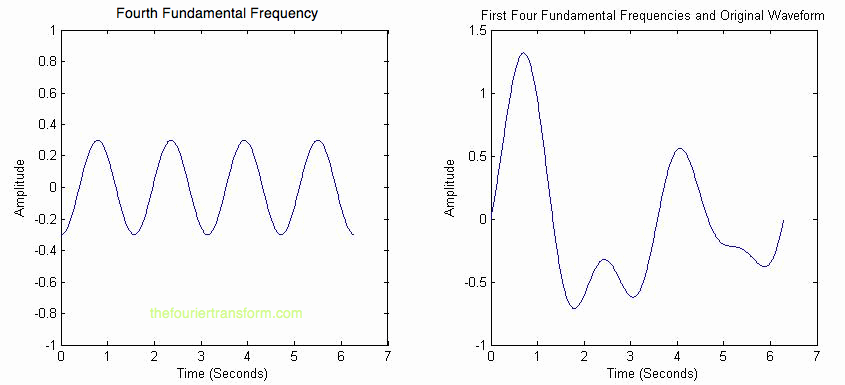
While this seems made up, it is true for all waveforms. This goes for TV signals, cell phone signals, the sound waves that travel when you speak. In general, waveforms are not made up of a discrete number of frequencies, but rather a continuous range of frequencies. The Fourier Transform is the mathematical tool that shows us how to deconstruct the waveform into its sinusoidal components. This has a multitude of applications, aides in the understanding of the universe, and just makes life much easier for the practicing engineer or scientist. To begin the study of the Fourier Transform, we will start by learning something very related - the Fourier Series. Next: Fourier Series Top: The Fourier Transform Fourier Transform Introduction Video Lecture About this Site: The Fourier Transform has always been a fascinating subject for me, and it is this excitement that leads me to present this Fourier Transform tutorial. In my life, I have found that once I thoroughly understand a subject, I am amazed at how simple it seems, despite the initial complexity. This I have found true for a wide range of activities, be it riding a motorcycle, learning the Fourier Transform, or understanding physical phenomena such as electromagnetics. With that in mind, I endeavor to write this Fourier Transform tutorial in the simplest of all possible manners. Specifically, consider this statement: Complexity is not a sign of intelligence; simplify. I have found this to a priceless amount of wisdom. In that regard, one need not know the intricacies of Lebesgue integration or complex integrals involving Cauchy residues in order to fully understand the Fourier Transform. The Fourier Transform is best understood intuitively; after all, physicists have long declared that all matter is actually waves (de Broglie's postulate), or a waveform-type phenomenon. The Fourier Transform, in essence, consists of a different method of viewing the universe (that is, a transformation from the time domain to the frequency domain). And since, according to the Fourier Transform, all waves can be viewed equally-accurately in the time or frequency domain, we have a new way of viewing the world. And this view is sometimes much more intuitive and simple to understand than the initial domain view. With that said, I am excited to begin this tutorial on the Fourier Transform. In these pages you will not find rigorous mathematical analysis on when and when not the Fourier Transform exists; I simply state the fact: all waveforms that arise in real-life (i.e. in nature, on your computer, in your network analyzer, sound, light, radio waves, etc etc) have Fourier Transforms. And as an engineer, the ultimate goal is to apply knowledge to the real world, not argue about mathematically obscure points. Hence, I frankly don't care about the waveforms for which the Fourier Transform does not exist; I know that I won't encounter one in practice and therefore I do not care. Not only does the Fourier Transform give us a special insight into how the world works, it shows up in real-world applications such as MRI (magnetic resonance imaging), signal processing, electromagnetics, quantum physics, and theoretical mathematics. As such, I can think of no serious scientist or engineer who could justify a career without knowledge of the Fourier Transform. On these pages, I will endeavor to make the study of the Fourier Transform as intuitive and math-less as possible; however, integrals invariably arise, so a refresher on calculus may be advised. About Me: I am a practicing engineer, having a PhD in the subject and work for many years in defense, university and the consumer electronics field. My background and work experience has interwoven signal processing, medical imaging and linear system theory, all of which bring up the recurring theme of the Fourier Transform. In addition, having taken Fourier Transform classes by professors with a passion for the Fourier Transform, this passion has been transferred to me. And my electromagnetics/antennas knowledge would be gapingly incomplete without a thorough understanding of the intuition and practice of the Fourier Transform. Fourier Transform joke: What did the Fourier Transform of the triangle pulse say to the Fourier Transform of the sinc function? Answer: You are such a square! While the above is only funny if you already know a little about the Fourier Transform, then I will consider it a success if this website at least teaches you enough about Fourier Transforms such that this is understandable. Contact the Author: pjbevel@gmail.com The work on this Fourier Transform tutorial is copyrighted. The page can be referenced and used at will, just cite the work if you use it. Copyright 2010-2022 TheFourierTransform.com. Home: Fourier Transforms