Fourier Series - Mean Squared Error (MSE)

Let's say you have two vectors, x=[1 2 1]=[x1 x2 x3], y=[0 -1 3]=[y1 y2 y3]. How do we know how close x1 is to x2? We could look at the distance (also called the L2 norm), which we write as: [Equation 1] For x and y above, the distance is the square root of 14. So for vectors, it's pretty simple to define some sort of distance. How do we do this for functions? It turns out it is exactly analogous. Suppose we have two functions, f(t) and g(t), defined over t=[0,T]. What is the distance between f and g? In a sense, we want to take the squared difference of each component, add them up and take the square root. This can be done via the use of the integral: [Equation 2] Note that the double brackets ||f-g|| means "the norm of f-g" (a norm, or a metric, is a distance between two things). We use the absolute value in equation [2] so that the norm is defined for complex functions, in case we felt like working with those. This "distance" is also known as the Mean Squared Error (MSE). This is an important metric in mathematics for defining convergence. Specifically, we are interested in knowing about the convergence of the Fourier Series Sum, g(t) (equation [3]), with the original periodic function f(t): [Equation 3] To get an idea of the convergence, let's define the finite fourier series, gN(t): [Equation 4] The function gN(t) is the first 2N+1 terms of the Fourier Series. 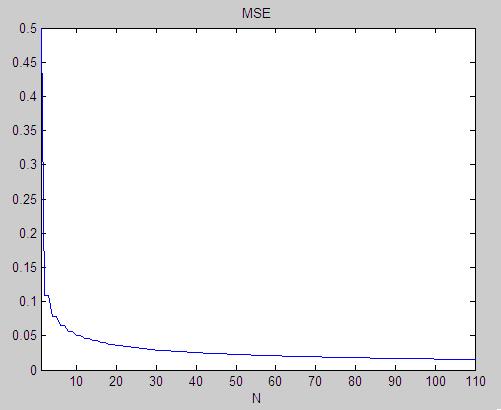We are interested in the distance (MSE) between gN(t) and f(t). This will be a function of N (the higher N is, the more terms in the finite Fourier Series, and the better the better the approximation, so the mse will decrease with N): [Equation 5] This is a function of N. The higher N gets, the more terms are in the finite Fourier Series gN(t), and the closer gN(t) will be to f(t). To give an idea of the convergence, let's look again at the square function from the complex coefficients page. Using the Fourier Coefficients found on that page, we can plot the mean squared error between gn(t) and f(t): Figure 1. The Mean Squared Error between gN(t) and f(t). It can be seen from Figure 1 that the finite Fourier Series converges fairly quickly to f(t). We had already observed this via the Figures on the real Fourier coefficients page. The MSE gives us a numerical way of viewing the convergence. In addition, mathematical proofs that the Fourier Series converges to the original periodic function make use of the MSE as defined here. In the next section, we'll look at deriving the optimal Fourier Coefficients (that is, the proof for equation [3] on the complex Fourier series coefficients page.