This page will show us how to get the Fourier Transform of an arbitrary function g(t) multiplied by t.
We just need to ensure that G(f) exists, and this result holds.
This can be done with a simple trick involving interchanging the order of integration and differentiation. Start
with a function g(t) and it's Fourier Transform G(f) and take the derivative with respect to frequency:
|  |
[Equation 1] |
Hence, we can re-arrange terms in Equation [1] to get the final result:
| 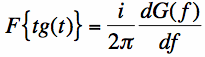 |
[Equation 2] |
It's that simple! This can be used to derive other Fourier Transforms.
We can use the same trick to find the Fourier Transform for t^n * h(t). Just assume n is a positive integer, and
that the Fourier Transform of h(t) is H(f).
Then:
|  |
[Equation 3] |
And the result follows:
| 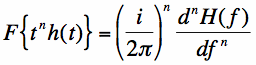 |
[Equation 4] |