Light: Diffraction, Interference and Young's Experiment
The jury has been out on that question for hundreds of years. Physicists have basically come to the agreemeent that
light is both a particle and a wave, depending on which experiment you are performing.
In this section, we will describe Young's slit experiment, which suggests light is a wave. And waves are
just functions, and functions have Fourier Transforms. We'll see a great application of Fourier Transforms
in the physical world: the viewing of the Fourier Transform of light for a particular case.
Before jumping in, let's discuss light a little bit.
Light is an electromagnetic wave. This is the same type of wave that the sun heats the earth with, that your microwave
warms your food with, and the exact same type of wave that is used by radios, televisions and your personal cell phone
to send information. As an electromagnetic wave, light waves have an electric and a magnetic field associated with it.
In addition, light waves of all types travel at speed c=300,000 km/s. The frequency f and
wavelength (lambda) of light satisfy the following equation:
In addition, we will assume that light behaves as a plane wave. This means that if the light is propagating
in the +z-direction, than the E- and H-field will be in the x-y plane. That is, the E-field associated
with a plane wave travelling in the +z-direction can be written via the vector:
Equation [2] shows that the E-field is modeled as a vector quantity. The magnitude is given by
some constant E_0, and the E-field "points" in the x-direction. The vector
In addition, the E-field is oscillating and a frequency f (hence the time dependence ft).
For light, the frequency is very high: 400-800 THz (or 4-8 * 10^14 cycles/second). The only difference
between light waves and the waves your cell phone emit is the frequency of the wave (cell phones
operate between 800-2100 MHz, or 8-21*10^8 cycles/second).
You might question: how good is the plane wave approximation? For light waves, it is fantastic.
Electromagnetic waves behave like plane waves when they are many wavelengths from the source, and also
the distance from the source is significantly larger than the physical size of the source. Since the wavelength
is so small, the first condition is virtually always satisfied. The second condition is true
as long as you're not too close to a light source, which is often the case as humans don't like to be right up
against their lights. In any event, it is simple to set up a plane wave, and that's what we'll need for
our analysis and experiment.
What's that? You would like to know more about electromagnetic waves? Feel free to cruise over to
antenna-theory.com for more information.
In the next section, we'll look at how a plane wave behaves when it hits a small opening in an aperture (a slit).
Is light a particle or a wave? Light
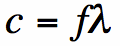
[Equation 1]

[Equation 2]
 is a unit vector in the +x-direction. The complex exponential in Equation [2] represents the
phase of the wave. Note that the wave is travelling in the +z-direction, and this is the
only spatial dimension that gives rise to phase change.
is a unit vector in the +x-direction. The complex exponential in Equation [2] represents the
phase of the wave. Note that the wave is travelling in the +z-direction, and this is the
only spatial dimension that gives rise to phase change.
Next: Light Through a Slit
Fourier Transform Applications
The Fourier Transform (Home)